Éjszakai őrség

Mindenki emlékszik, hogy volt az a bizonyos megoldóképlet a másodfokú egyenlet gyökeire.

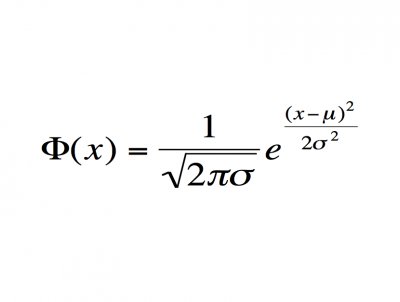
Ja, ez nem is az. Inkább ez. :)

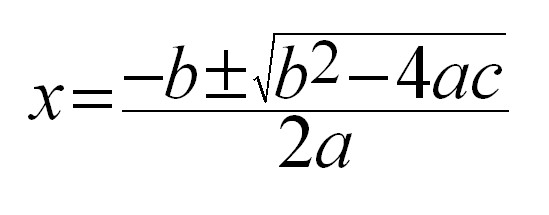
És ugye ezerrel a szánkba lett rágva, hogy egyrészt az a nem lehet nulla, mert akkor nem másodfokú az egyenlet, és különben sem nagyon illik nullával osztani. Bár egyes hírek szerint Chuck Norris még ezt is tudja. Másrészről pedig a gyökjel alatt csakis pozitív szám állhat, különben nincs az egyenletnek valós gyöke.

Páran ugyan elgondolkodtunk rajta középiskolában, hogy mi a francot jelenthet az, hogy az egyenletnek nincs valós gyöke, de a szűk keretek miatt ezt a témát akkor nem nagyon tártuk fel, nyitott maradt tehát a kérdés, a bogár meg be volt ültetve a fülünkbe ami aztán a legtöbb esetben ki is mászott onnan, boldogságban hagyva a fül gazdáját.

Abban a szerencsében volt részem, hogy sikerült felsőbb matematikát is hallgatnom. Ez az egész poszt arról a katartikus élményről szól, amikor végre megtudtuk az igazságot a nem valós gyökökről. És most arra kérlek, hogy ne add fel az olvasást, rá fogsz jönni, hogy a matek szép, érthető, és vallásos ámulattal fogsz tekinteni arra, aki anno kitalálta azt a modellt, amiben nem foglalkozunk azzal, hogy egy szám pozitív vagy negatív, és ha úgy adja a sorsunk, hát simán gyököt vonunk belőle.

Picit alapozzunk azért, mégpedig a számhalmazokkal.

Ezek a természetes számok: 0, 1, 2, 3, 4, .... Ezek az egész számok: ... -4, -3, -2, -1, 0, 1, 2, 3, 4.... Ezek a racionális számok: 0,5, -603,8, 50, 3/4, 2/3, azaz olyan számok, amiket véges számú számjeggyel vagy két szám hányadosaként le tudunk írni. A 3.14159265359 is racionális szám, még ha az eleje miatt gyanúsnak is ítéljük, mert ez ugye csak egy nem végtelen hosszú számsorból álló, úgynevezett tizedes tört. Van aztán még egy érdekes halmaz, az irracionális számok halmaza. Furcsa alakok, mert ki gondolná, hogy egy olyan szép alakú valami, mint a kettőnek vagy a háromnak a négyzetgyöke nem racionálisak, pedig ezek ráadásul frankón szerkeszthetők is.

Nos, ezeket a számokat, amiket felsoroltam, több dolog is összeköt. Ezek közül az egyik, jelen kérdés szerint legfontosabb, hogy ha bármelyik számot saját magával szorzom, akkor egy pozitív számot kapok. Azaz ha négyzetre emelem a gyökkettőt, a hármat, a 0,666666-ot, az eredmény annyi lesz, amennyi, de mindig pozitív lesz. Vágjuk még ugye a mentő kérdést:

Hol vannak hát akkor azok a számok, amiket saját magukkal megszorozva negatív számokat kapunk? Hát lássuk.

A fent felsorolt összes fajta számot ha tekintjük, őket egy üstben valós számoknak nevezzük. Mi akadályoz meg bennünket abban, hogy ezekből a számokból számpárokat képezzünk? Semmi. Ha leírom azt, hogy (3, 5), el tudom olvasni, (-2, 2/3) sem okoz gondot, de a (0, 0) sem.

Ha jobban megfigyelitek, amikor felsoroltam a számok típusait, egyre bővülő halmazokat soroltam. Először a pozitív egészek voltak (a természetes számok), aztán az egész számok, amikbe benne voltak a természetes számok is, aztán jöttek az ezekből mindenféle művelettel előállítható racionális számok, majd az irracionálisak. Mindegyik halmaz tartalmazta az őt megelőző valamennyi számot.

Definiáljunk most egy bővebb halmazt, mint a valós számok úgy, hogy abban az eddigi összes szám benne van, és az addig elvégezhető műveletek is mind megmaradnak értelmezhetőnek, depláne ugyan azt az eredményt adják, mint eddig, azaz a 3 + 3 itt is 6 lesz, a 8 * 8 pedig továbbra is 64. Tehát számpárokat fogunk most használni, mégpedig nem is akármilyeneket, hanem rendezett számpárokat, ami csak annyit tesz, hogy az (1, 2) nem egyenlő a (2, 1)-gyel. Ezeket a számokat pedig komplex számoknak nevezzük el, a számpárt alkotó számokból az elsőt a komplex szám valós részének, a másodikat pedig képzetes (imaginárius) részének hívjuk. És ennyi. :)

Jól látható, hogy a (4, 0) komplex szám az a 4-et jelenti, a (2/3, 0) a 2/3-ot, azaz az összes valós számot frankón le tudom írni számpárokkal is, épp csak a képzetes részbe nem írok semmit. Dehát "Nomen est omen", a valós szám pont azért valós, mert nincs képzetes része.

Már csak annyi van hátra, hogy értelmezzük a műveleteket ezeken a számpárokon, és most előre szólok, tessenek megkapaszkodni.

Ki nem hinné, hogy (1, 0) + (1, 0) = (2, 0)? Hiszen 1 +1 = 2. Nem igaz? (2, 0) * (3, 0) = (6, 0). Ha nem érted, akkor nem figyeltél, jössz egy sörrel. Nem sokkal bonyolultabb ez sem: (1, 1) + (1, 1) = (2, 2). Pedig itt már képzetes rész is szerepel. És ne hidd, hogy a kivonás ettől bonyolultabb. Házi feladatként sem adnám fel, mert egy perc alatt megoldod.

A zsenialitás a szorzás definíciójában van. Most (a₁, b₁) és (a₂, b₂) alakban írom le a két komplex számunkat, hogy jól követhető legyen, mit is művelünk.

Figyelem, nem megijedni, tanulmányozni! Elöl is két számpár van, összeszorozzuk, egy számpárt kapunk. 5* 6 = 30. Pont ahogy az összeadásnál is volt, két számból egy lett. Csak a szorzásnál kicsit több elemmel írtuk le az eredmény számpárt, de ennek oka van.

Nézzük meg konkrét példával. Az 5 * 1, akárhogy is nézzük, csak 5 lehet. Az 1-et ugye úgy írjuk, hogy (1, 0). Lássuk, igaz-e. Alkalmazzuk a fenti képletet. Kiírom részletesen.

(5, 0) * (1, 0) = (5*1 - 0*0, 5*0 + 1*0) = (5, 0)

A vak is látja, hogy elvégezve a szorzásokat (5, 0) lesz az eredmény, azaz 5 * 1 az tényleg 5. Vagyis örülünk!

Azt állítom, hogy a (0, 1) komplex szám, amit az (1, 0) valós egység mintájára imaginárius egységnek, i-nek nevezünk, egy olyan szám, hogy ha őt négyzetre emelem, akkor eredményül -1-et fogok kapni. Lássuk! (Izgulok, hogy kijön-e.)

Szorozni kell tehát a (0, 1) -et önmagával, mégpedig a fenti definíció szerint.

(0, 1) * (0, 1) = (0*0 - 1*1, 0*1 + 0*1) = (-1, 0)

Vagyis az eredmény (-1, 0), egy nagyon is valós szám, képzetes rész nélkül. Uram isten, -1 lett a négyzete az imaginárius egységnek!!

Itt a vége.

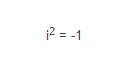
És ezt így is írhatnám, ha mindkét oldalból gyököt vonok.

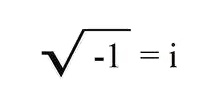
Hát nem csodálatos?

(És itt a végén bocsánatot kérek a bulváros címadásért, az most egy közösségi média teszt része is. Két legyet egy csapással.)