Éjszakai őrség

Na, ez filozofikusan hangzik. Nem egyszerű az ember dolga, ha erről magyarázni kell, főleg sörözés közben nem. Az alábbi forgatókönyv azonban működött.

Jó kiindulási alap, ha elkezdi az ember a természetes számokat soroltatni 1-től (vagy ha úgy tetszik, 0-tól) unásig, és közli, hogy ez aztán elmehet a végtelenségig, de NEMADDIGA! Mert ezt megszámolhatóan végtelennek mondjuk, meg az összes ilyen típusú mennyiséget, ami ezzel egyértelműen összefüggésbe hozható. És hozza az ember a példának okáért mindjárt azt, hogy ugyanannyi páros szám van, mint páratlan, borzolja a kedélyeket azzal, hogy ugyanannyi páros van, mint hattal osztható, sőt, ugyanannyi az egész számok számossága, mint a százzal oszthatóké, stb. Egészen vicces szemöldököket lehet már ilyenkor látni. A frappáns bizonyítás után meg még inkább.

A probléma iránti fogékonyság néha generálja a "Hö! Akkó nem megszámolható végtelen is van?" kérdést, de ha nem, hát elő kell vele jönni, és mindjárt példálózni is illik a valós számokkal, megmagyarázva, hogy mik a valós számok. (Nem matekosok kedvéért: valós számok pl. a nem egész számok, meg a Pi, meg a gyökkettő, stb.) Itt már azért elfogy az éppen aktuális sör, és további színezést ígérve egy körre még tuttira be lehet nevezni. A hallgatóság hite ott fogy el először, amikor közöljük, hogy 0 és 1 között márpedig több szám van, mint az összes egész számok, pozitívak és negatívak, a nullát akár hozzávéve, akár nem, ő itt éppen nem oszt, nem szoroz. Egyébként szoroz, ha már a szójátékoknál tartunk, de az osztás... Hát azzal van egy kis anomália. :)

Mi jöhet még? A continuum probléma említése kötelező (létezik-e számosság a megszámlálható és a megszámlálhatatlan végtelen közt), és itt az algebrai vonalat célszerű is befejezni, mert a sok sör ellenére is száraz kezd lenni a téma. Jöhetnek a grafikus érdekességek.

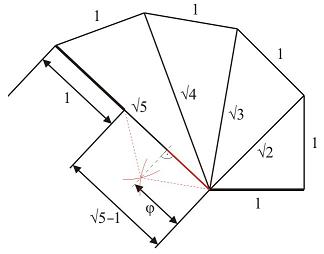
A végtelen egyik érdekes megjelenése, ha mondjuk az egyharmadot (0,333333...) vagy a gyökkettőt (1.414213...) próbáljuk megmagyarázni, utalva erősen arra, hogy míg a világ, és két sör, addig se tudnánk leírni az ilyen számok számjegyeit, annyian vannak. De ha megmutatjuk, hogy pl. a gyökkettő, gyökhárom, stb. hosszúságokat igenis meg lehet szerkeszteni, az már elismerést vált ki, még ha a "Na, erre nem gondoltam volna" típusú homlokraütések sora bontakozik ki ahelyett, hogy "Jau van ecsém, a következő körre vendégem vagy". :( Az ábrán az aranymetszés nevezetes arányszámának megszerkesztése mellett épp ilyen kis okosságokat mutatnak meg. (A Wikipédiából nyúltam.) Az aranymetszésre most inkább nem térnék ki, pedig ugye már a régi görögök is...

Még cifrább, de ezt már tényleg nem szokják elhinni, ha mutatunk egy olyan vonalat, ami ugyan elfér a papíron, a hossza azonban semmilyen határok közé nem szorítható, konkrétan végtelen. Több ilyen vonal is van, igen, konkrétan végtelen számúan vannak - házi feladat: milyen végtelen? :) - de az egyik leglátványosabb közülük az úgynevezett Koch görbe. Egy vonalból indul ki, amit megharmadolunk, a második harmadot kitöröljük és helyébe a kitörölt szakaszból (pontosabban kettőből) kis házikót teszünk, majd ezt folytatjuk a végtelenségig a keletkezett szakaszok mindegyikén. Lásd az animációt.

Ha ezt a rajzolást háromszögből indítjuk annak mindegyik oldalára, a Koch-hópehely alakzathoz jutunk el. Azt a képet nem teszem be ide, nézzétek meg a fenti linken.

És most jöhet a kegyelemdöfés, bedobhatjuk a fraktál című varázsszót. Mert ez a vonal ugye már az, per definíció. Kicsit pongyola lesz a megfogalmazás, de mindenki megérti, ha úgy tálaljuk, hogy fraktál az, amit valamilyen szabály vagy szabályok sorozatos végrehajtása után kapunk, és az ábra lépésről lépésre lesz egyre bonyolultabb, részletgazdagabb. A szabályosság leginkább a Koch görbénél látszik, a részletgazdagságra azonban az úgynevezett Mandelbrot halmazokról készült képeket javaslom. Az elméletről a Wikipédia tudományos igényű leírásánál sokkal pontosabbat kár idézni.

Azt modja minderre az egyik tag: öregem, én ettől egyszerűbben elmagyarázom a végtelenek közti különbséget. Idézem.

Az alkesz találkozik a jó tündérrel. Vagy aranyhallal, mindegy, csak legyen neki három kívánságos opciója. Azt mondja:
- Hát te igen szerencsés ember lettél volna józanul, de a kollektív szerződés értelmében a te kívánságodat is teljesítenem kell. Én azonban sztrájkolok, és csak két kívánságra mérsékelem az elégséges szolgáltatást, szóval mondjad.
- Hááát... Kellene egy üveg, de olyan, amiből sose fogy ki a sör.
Csiribí, csiribá... És ott a sör. Örülnek mindketten, az alkesz is, de rendesen. Kérdi a tünci, hogy mi legyen a második, és egyben utolsó kívánság. A szerencsés belekortyol az üvegbe, látja, hogy tényleg működik, nem fogy ki, majd így szól.
- Akkó... Ebből kellene még egy üveg.

Na öcsém, mondja a tagunk, az üvegek a megszámlálható számosság, a sör meg a nem megszámolható. Vágod? Itt nincs jó válasz. :)

És hogy miért mondtam mindezt el? Mert találtam egy nagyszerű Mandelbrot halmaz generáló programot, és annak kapcsán eszembe jutott, hogy a kocsmában nem volt nálam egy darab laptop se (még szép), amivel az ebből kifolyó képeket megmutathattam volna. Itt van: http://sourceforge.net/projects/quickman

Két képet azért mutatok a végére, klikkre megnagyobbodnak.